Polyhedra in History: Part-1 (Göbekli Tepe - Etruscans)
- Aarsh Batra
- Aug 15, 2021
- 27 min read
Updated: Aug 22, 2021
Harold Scott Macdonald Coxeter, one of the greatest geometers of the 20th century, in his book, Regular Polytopes (ref 1), wrote:
"The early history of these polyhedra is lost in the shadows of antiquity. To ask who first constructed them is almost as futile to ask who first used fire"
Coxeter was right, it is probably futile to invest time in exactly pinning down the person who first constructed polyhedra. But, having said that, here is something that is not futile (and actually quite worthwhile, as we will see): In tracing the history of polyhedra, instead of trying to pin down the exact person who constructed the first polyhedra, we will go back in time to as far as the archaeological evidence takes us and move forward from that point. This is the best we can do in our effort of tracing the history of polyhedra. This will take us back in time 11,500 years (9500 BCE) and from there we will move forward to the present times.
The knowledge of conceptualizing and constructing polyhedra is either sustained or (in other cases) continuously rediscovered through out history across various cultures and geographies. In some other places, we see that Polyhedra appear sporadically, an example is the Medieval Islamic world (ref 2). We will (chronologically) explore all of this and much more in this four part series of blog posts called: Polyhedra in History.
In these posts, I attempt to trace the origins of various polyhedra in an exhaustive manner. I will look into all available Archaeological (and other) evidence available on polyhedra. In doing so, we will explore polyhedral motivations in: Architecture, Jewelry, Mesopotamian accounting tokens, an Iranian grave of a burnt and abandoned city among other sources. If there is a possible polyhedra origin story in history, I will hunt that down.
For each of the polyhedra we find in various points in history, we will learn about its geometry and how it relates to other Polyhedra, which family does it belong to and much more. Along the way, I will shed light on the major figures/cultures in history who devoted extensive time to studying, making and providing Mathematical descriptions of these polyhedra.
In Part-1 we will start exploring the earliest polyhedra motivations (in the form of cube and cuboidal structures) in the earliest human made structures like the Göbekli Tepe, c. 9500 BCE (11,500 years ago), a Neolithic archaeological site near the city of Şanlıurfa in Southeastern Anatolia, Turkey. From there we move on to exploring the polyhedra of the Egyptian civilization in ~5000 BCE (~7000 years ago) and move forward in time ending at the Etruscan civilization (900 BCE - 500 BCE).
In Part-2 will start exploring the Greek civilization (from 460 BCE - 320 CE). Greeks contributed extensively to the study of polyhedrons. They were the first to provide a Mathematical description of these objects and contributed extensively towards the field, continuously for a millennia. In this part we also look at a few isolated examples of Polyhedra that appear sporadically elsewhere (Ancient Egypt, Elephantine Egypt, Greco-Roman Egypt, Roman civilization, Ancient Chinese, etc.) during the Ancient Greece era (12th century BCE - 6th century CE). This will take us to 7th century CE.
Part-3, starts in the post Ancient Greece period exploring the Polyhedra of the Medieval Islamic world (starting from 800 CE) and moving on to exploring the plethora of polyhedra artists of the Renaissance (15th and 16th century CE).
Finally Part-4 (last part of the series) starts from Post-renaissance (beginning of 17th century CE) and move forward to the present times.
Please Note: While tracing polyhedra in history, I will introduce and explain new concepts. Many topics that will come up, ideally deserve a separate blog post of their own to be properly discussed. For such topics, I will write separate blog posts in the future. For the purposes of this series (in which our focus is on tracing the history of Polyhedra) I will briefly touch on and explain various concepts, which will get their separate individual attention in posts that will follow the polyhedra in history series of blog posts. I encourage the readers to share their suggestions (about specific topics in these posts that you would like to be more comprehensively explored) in the comments section.
The earliest known written record of polyhedra comes from Classical Greek authors who also gave a Mathematical description of them. But, archaeological findings shows us that enquiry into polyhedra for meeting artistic and architectural ends, started much earlier and dates back to as early as 9500 BCE (11,500 years ago). On the other hand, the earliest evidence of Mathematical enquiry into polyhedra can be traced back to the Egyptian civilization (1850 BCE, ~3850 years ago).
Making of a polyhedra, with building materials (or in art) requires substantial knowledge of its geometry. Various civilizations before Greeks were intimately familiar with the geometry of various Polyhedra, but it were the Greeks who were the first to view polyhedra as an entire field (or a subfield of Geometry) of Mathematics, to be studied in and of itself. Before the Greeks, enquiry into polyhedra was more artistic than Mathematical and limited to specific contexts (examples of contexts include: Architecture, Gaming, jewellery, Art etc.) and was not properly studied as a Mathematical Discipline in and of itself. Greeks were the first to view polyhedra as a field of study (a discipline), one that they rigorously investigated.
One thing that remains true for everyone (irrespective of the fact of whether the enquiry was Mathematical or purely artistic), including Greeks, their predecessors, and their successors is aptly summarized in the following quote by Coxeter:
"The chief reason for studying regular polyhedra is still the same as in the time of the Pythagoreans, namely, that their symmetrical shapes appeal to one's artistic sense"
With the above quote in mind, we trace the history of polyhedra by going back in time to 9500 BCE (11,500 years ago) to one of the first manifestations of human made monumental architecture, the Göbekli Tepe. Göbekli Tepe is a Neolithic archaeological site near the city of Şanlıurfa in Southeastern Anatolia, Turkey.
Dated to the Pre-Pottery era, between c. 9500 and 8000 BCE, the site comprises a number of large circular structures supported by massive stone pillars – the world's oldest known megaliths.
A megalith is a large prehistoric stone that has been used to construct a structure or monument, either alone or together with other stones. The image shown below is one of the megalith pillars (pillar 18, Building D) from Göbekli Tepe, on which some stabilization work is being performed.
The slabs that went into making of these limestone pillars were transported from bedrock pits located approximately 100 metres (330 ft) from the hilltop, with workers using flint points to cut through the limestone bedrock.
In these structures (pillar number 18 above), we see the most early form of polyhedral motivations in the form of shapes (of the various megalithic pillars) that are roughly hexahedrons. In most cases they are roughly cuboidal (a cuboid is a polyhedron made up of 6 quadrilateral faces) structures with 6 faces.
A Hexahedron is any polyhedron with 6 flat faces.
On the other hand, a regular hexahedron (more commonly known as a Cube) is the one in which each (of the total 6) faces is a square, and where three square faces meet at each corner (vertex).

These Hexahedrons crop up in some of the oldest surviving architecture, elsewhere in the world at different points in time. A few examples are as follows:
Tarxien temples of Malta.
Dolmens: a type of single-chamber megalithic tomb, usually consisting of two or more vertical megaliths supporting a large flat horizontal capstone or "table".
Dolmen of Menga, a megalithic burial mound called a tumulus, a long barrow form of dolmen, dating from the 3750-3650 BCE approx. It is near Antequera, Málaga, Spain.
Dolmens of North Caucasus in Russia.
Ġgantija (3700 BCE), a megalithic temple complex from the Neolithic times on the Mediterranean island of Gozo, in Malta.
The architects from these early human settlements would probably not have realized that in making such roughly flat faced pillars out of stone, they were setting the foundations of artistic enquiry into the world of polyhedra.
Moving forward in time to the Pre-Dynastic period (5000 BCE - 3100 BCE, approximately 7000 years ago) of Egypt, we find tombs, called Mastaba (plural Mastabas, precursor to the Pyramids), which take the form of a flat-roofed rectangular structure with inward sloping sides constructed out of mudbricks. These edifices, marked the burial of many eminent Egyptians during that time.
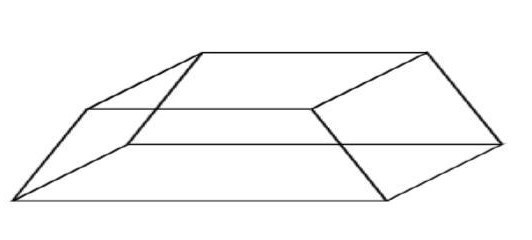
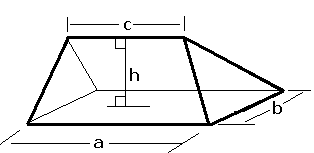
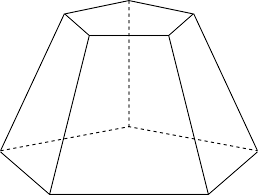
Mastabas are similar to a family of Polyhedra called Frustums (singular: frustum). A polyhedron belonging to the frustum family contains two similar (but not congruent) polygons (called 'bases') that face each other, with their corresponding vertices (corners) connected to each other by straight lines, which makes the rest of the faces (other than the two bases) trapezoids. Given an infinite number of possible base polygons, an infinite number of frustums are possible, each distinguished (and named) given its base polygon.
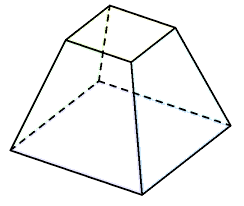
In the above example, we saw a Frustum with a Trapezoidal Base. Another example of a polyhedra from the frustum family is a frustum with a Square base. This looks like an Egyptian Pyramid (see below) that is sliced from the top. In general, all polyhedra that belong to the frustum family, are cut out portions of some other Polyhedra. Below is an example of a frustum with a square base.

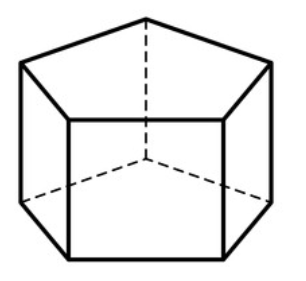
In general, the frustum family of polyhedra is a subset of a family of polyhedra called Prismatoids. A polyhedron belonging to the prismatoid family is recognized as follows: all of its vertices (corners) lie in 2 parallel planes. Other than the frustum family of polyhedra, the prismatoid family includes these other families of polyhedra: Pyramids, Wedges, Parallelepipeds, Prisms, Antiprisms, Cupolae. All of these aforementioned families are part of the prismatoid family of polyhedra.
Ahead in this blog post, we will see Polyhedra in history from three of these above Prismatoid families: Pyramids, Parallelepipeds and Prisms. The rest of the families of polyhedra will be discussed in greater detail in a separate blog post. Below mentioned are examples of polyhedra (one example each for each family) from all of the above families.
Egyptian Mastabas were pre-cursor to the Egyptian Pyramids (a polyhedron that we will explore in greater detail ahead in this post). The first Mastaba appeared at least 2300 years before the first Pyramid (Pyramid of Djoser in 2670 BCE).
Before we get to the Pyramids, we travel North-West from Egypt to Mesopotamia, specifically: Tepe Gawra (in Iraq). Here, accounting tokens ( from around 4000 BCE) have been excavated. In ancient Mesopotamia, almost 10,000 years ago, scribes started using counters, to represent certain quantities, units or goods (ref 3). Thousands of these tokens have been found in archaeological sites across the Middle East. The ones excavated at Tepe Gawra come in variety of shapes, of which one is roughly a Tetrahedral token (second from the left in the below image).
A Tetrahedron is a polyhedron composed of 4 Triangular faces, 6 straight edges and 4 vertex corners). A regular tetrahedron is a tetrahedron in which all four faces are equilateral triangles.
Later on (around 3200 BCE) these counters, were pressed into clay tablets (while the clay was still soft) to create a lasting record. Two such tablets, from Susa in Iran (created around 3200 BCE) are shown below.
Triangular and Circular impressions can be clearly seen on the tablets. These simple markings, laid the foundation for Cuneiform, one of the first writing systems in History.
One important thing to note is the following: A Tetrahedron has a triangle at its base. The Pyramids at Egypt are not Tetrahedrons (more detail later in the post), because they have a square base. In other words, a Tetrahedron is a pyramid whose base, and also all other faces are triangles.
Next stop in our hunt for polyhedra takes us to Kincardineshire, a historic county on the coast of Northeast Scotland. The solids found here were carved sandstone balls, roughly 3 inches in diameter, dating back to (c. 4000 BCE - c. 1400 cal. BCE) and are currently at display in the Ashmolean Museum at the University of Oxford (ref 4).
The knobs (the rounded bulges) in the above balls are roughly comparable to the vertices (corners) of a polyhedron. Furthermore, if we connect the midpoints of all the knobs (connecting each midpoint to the its adjacent midpoint in all directions by straight lines, that cut through these balls), the resulting skeleton is a polyhedron.
Next, we look at the Step Pyramids that have shown up in various places in History. These structures were similar to the Trapezoidal Prisms that we saw earlier in this post. They look like various Trapezoidal base frustums stacked one over the other, with the highest one having the smallest base area. Egyptian Step pyramids were the pre-cursor to the "True Pyramids" (with smooth sides and a pointed apex).
In the First Dynasty at Saqqara (beginning around 3100 BCE), a large step pyramid like structure was found within the interior of Mastaba 3808 dating to the reign of the pharaoh Anedjib. This is supposedly the first step pyramid of Egypt, and is considered by some Egyptologists as the forerunner of the Step Pyramid of Djoser (earliest colossal stone building in Egypt).
Step Pyramids are not confined to Egypt. Mesopotamian Ziggurats were huge religious monuments, built in ancient Mesopotamian valley and western Iranian Plateau, having the form of terraced step pyramid of successively receding stories or levels. The oldest Ziggurat is the Sialk Ziggurat in Kashan, Iran, which dates back to early third-millennium BCE. There are 32 Ziggurat known at and near Mesopotamia. Some notable ones include the Great Ziggurat of Ur, near Nasiriyah, Iraq, the Ziggurat of Aqur Quf near Baghdad, Iraq.
The step pyramid of Great Ziggurat of Ur is a frustum with a Trapezoidal base (the same shape that we saw above in the Egyptian Mastabas). Furthermore, if we look closely, we notice another polyhedra at its entrance. The staircase of the Ziggurat, is shaped like a right triangular prism.

Earlier in the blog post, we learned that, prisms is a family of polyhedra that itself belongs to the prismatoid family of polyhedra. A prism is a polyhedron comprising of a base that is a polygon, another base that is a translated copy of the first base, and the remaining faces are all parallelograms that join corresponding sides of the two bases without rotation. In the above example of the right triangular prism, the 2 bases are the two right angled triangles (one is an translated copy of the other) and the rest of the faces are rectangles. The right triangular prism is one of the infinitely many possible prisms (corresponding to the infinitely many polygon bases) in the prism family.
It is important that we note the distinction between frustums and prisms. Both prisms and frustums have 2 bases. But, in a frustum the 2 bases are not translated copies of one another. In a frustum, the 2 bases are similar polygons ( their sides are proportional in length) but not congruent. On the other hand, the 2 bases of prisms are congruent and translated copies of one another. To further clarify the distinction, in the image below, a pentagonal base prism is shown alongside a pentagonal base frustum.
Another step pyramid, dating back to 4000 BCE is present at the archaeological site of Monte d'Accoddi, in Sardinia, Italy. It is a trapezoidal platform on an artificial mound reached by a sloped causeway and is relatively much smaller in size than its counterparts in Egypt and Mesopotamia.
As we will see later in this series of posts, various civilizations and cultures at various points in time (after the Egyptians and Mesopotamians), built step pyramids. Some of the civilizations and places where these structures were built are: Mayans, Nsude Pyramids of Africa, South American Step Pyramids (Moche and Chavin culture), Step pyramids of North America, Cambodia and Indonesia (ref 5).
From Step Pyramids, we move to the "True Pyramids" of Egypt. In the Fourth Dynasty (starting around 2613 BCE, around 4600 years ago), the Egyptians began to build these pyramids with smooth sides and a pointed Apex. The earliest of these Pyramids, located at Meidum was first constructed as a finished "tower-shaped" step pyramid like structure and later converted to a true pyramid. Sneferu (the founding Pharaoh of the fourth dynasty of Egypt during the old kingdom) was responsible for converting the earlier step pyramid construction into the True Pyramid with smooth sides.
We have already seen a pyramid with a triangular base (Tetrahedron). The Egyptian Pyramids (like the ones built by Sneferu and his successors) are roughly Square base pyramids. In general, a Pyramid is a polyhedron, which contains a polygon for its base and the rest of the faces (total number of which depends on the base Polygon) are triangles, all meeting at a common point (the apex). Given the infinite number of possible polygon bases, infinite number of pyramids are possible.

Sneferu is also credited with building two other pyramids, the Bent Pyramid and the Red Pyramid at Dahshur, which were the first true pyramids to be built as such from the beginning. It was Sneferu's son and successor Khufu, the second pharoah of the fourth dynasty who is generally accepted as the pharoah who commissioned the construction of the Great Pyramid of Giza (ref 6).
The Bent Pyramid (top left in the above images) is not a typical Egyptian pyramid (see above), given the bend right around the middle of its height. It is more accurately defined as: a square base frustum (lower section) with a square base pyramid (upper section) sitting over it. The Bent Pyramid rises from the desert at a 54-degree inclination, but the top section (square base pyramid) is built at the shallower angle of 43 degrees, lending the pyramid a visibly 'bent' appearance. As a result, the Bent Pyramid is a Polyhedron with 4 triangular faces, 4 trapezoidal faces, and a square base. This distinguishes it from the typical Egyptian pyramid which has four triangular faces and a square base.
Our knowledge of Egyptian mathematics comes largely from the mathematical problems contained in the papyri that have been preserved by the dryness of the desert climate. Papyrus is a material similar to thick paper that was used in ancient times as a writing surface. It was made from the pith of the papyrus plant, Cyperus papyrus, a wetland sedge.
Peter R. Cromwell, in his book Polyhedra (ref 7), writes:
"These problems contain various problems of practical nature, ranging from plane geometry to solid geometry (volumes of cylinders, barns, beams, pyramids). It is generally accepted (on indirect evidence) that the Egyptians could find the volume of a pyramid, and that they also had a rudimentary notion of trigonometry which allowed them to express the degree of slope (or gradient) of a pyramid. Since the Egyptians did not possess a symbolic notation in which to express their formulae, they had to give a series of worked examples—special cases with particular numbers rather than the general case. The same example would be used in different contexts. For instance, problems 57 and 58 of the Rhind mathematical papyrus both deal with the same pyramid. In the former problem, the height and base are the data and the slope is calculated; in the latter, the height is the unknown quantity"
The fourteenth problem of the Moscow mathematical papyrus (dating to around 1803 BCE) is concerned with the volume of a truncated Pyramid (also known as the frustum). The papyrus itself is 8cm wide and over 5m long. It contains 25 problems, many of which are unclear because the papyrus is damaged. The text containing problem 14 is shown below. It is written in hieratic script, a simplified form of hieroglyphics.
How did the Egyptians discover their formulae and algorithmic procedures? We cannot properly answer this yet, since the papyri are not concerned with such things. They neither contain any motivation, nor any justification to validate the methods they describe. Their only motivations is to communicate the technique or rules to be followed in particular circumstances. The Egyptians did not possess a notation in which they could express general formulation of their results.
Cromwell further writes,
"This was a civilization who had no plus, minus, multiplication or division signs, no equals or square root signs, no zero, no decimal point, no coinage, no indices, and no means of writing the common fraction"
This lack of notation was overcome by giving several worked examples of a similar
nature using different numbers to illustrate the method of solving a particular
type of problem. They expected that the general procedure would be abstracted
from sufficiently many specific examples. But, description of procedures, cannot establish the universal validity of a formula (ref 8).
Babylonians (an ancient civilization from Mesopotamia) considered similar problems (around the same time, i.e. 1800 BCE) to Egyptians, namely problems concerning cones, pyramids, frustums etc. Their records were preserved in the form of Clay tablets, which were inscribed by wedge shaped signs by pressing a stylus into the soft clay. The script is now called cuneiform. Even, later ancient Chinese texts (dating to around first century CE) deal with similar problems. The oldest surviving and most influential of the ancient Chinese mathematics texts is the Chiu-Chang Suan-Shu (Nine Chapters on the Mathematical Art), a series of 246 problems together with their solutions.
The Mathematics of the Egyptians, Babylonians and the Chinese all shared similar features, most of their content is a description of a process, often given as a series of worked examples. It were the Greeks (as far as the evidence dictates) who were the first civilization to introduce a notion of proof in Mathematics. It is uncertain whether early civilizations originating in different places on the globe, could even formulate propositions in a general context. There are no traces of deductive arguments being used to justify methods in any pre-hellenic culture. The Greeks not only stated general propositions but furnished them with rational arguments to demonstrate their universal validity.
Greeks also contributed extensively to the study of Polyhedra. We will get back to them in the second part of this series of blog posts. But, still it is interesting to note that how much progress a civilization (like the Egyptians) can make with a lots of worked examples alone.
Moving back to Mesopotamia, a gaming board (Royal Game of Ur), along with its Tetrahedral dice (1.7 centimeters in length and width and 1.3 centimeters high) made of stone was found in the Royal cemetry at Ur and has been dated to 2600 BCE (~4600 years old).
Ur was an important Sumerian city-state in ancient Mesopotamia, located at the site of modern Tell el-Muqayyar in southern Iraq's Dhi Qar Governorate.

The regally adorned board (full of beautiful and intricate geometric patterns) along with its Tetrahedral dice (see below, the dice is placed in front of the board) is currently at display at the British Museum (Museum item # 120840).

We already saw the Mesopotamian Tetrahedral counting tokens from Tepe Gawra (4000 BCE). Now, we have a second context in which the Tetrahedron was used in Mesopotamia, namely as a gaming dice.
The Ur board is identical in form to the Burnt City board (a wooden backgammon like gaming board). The Burnt city board was found in Shahr-e-Sukhteh (meaning "The Burnt City") , an archaeological site in eastern Iran corresponding to an early Bronze age settlement.

The city was one of the world's largest cities. It appeared around 3200 BCE and burnt down three times before finally being abandoned in 1800 BCE.
Along with the wooden backgammon-like board, 4 parallelepiped shaped wooden dice and some other pieces were excavated from the graveyard (grave 731) of Shahr-e Sukhteh in an Italian expedition in 1970s. They have been estimated to be crafted around 2500 BCE - 2300 BCE (ref 9).



The board, the 4 elongated dice and 27 tokens were found lying inside a basket placed near the pelvis of a human buried in a pseudo-catacomb (grave 731).
These dice (dimensions (l, w, h): (1cm, 1cm, 3cm)) and tokens were used along a gaming board measuring 33.2 cm long and 12 cm wide, to play the Game of Twenty Squares, a two player strategy race board game that was popular in ancient Mesopotamia.
The following figures (Piperno and Salvatori 1983) schematically illustrate the board and the location in grave 731 where it was found:
The Burnt city dice were shaped as Parallelepipeds and rolled a number from 1 to 4. They had six faces but were numbered along only the four rectangular faces.
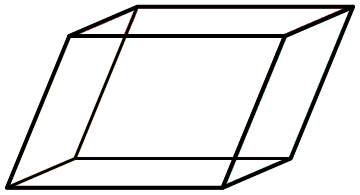
A Parallelepiped is a Hexahedron formed by six parallelograms. By analogy, it relates to a parallelogram, just as a cube (regular hexahedron) relates to a square. In other words, all cubes are parallelepipeds, but all parallelepipeds are not cubical.

The historical relationship and evolution of different 4-sided dice (4, refers to four numbered sides) is not yet comprehensively studied. However, by practical experimentation it has been found that grabbing a Tetrahedral Dice (one found in The Game of Ur) can be challenging, meaning the elongated (parallelepiped) dice is easier to grasp.
While the Game of Twenty Squares is the world's oldest known board game, its rules have been deciphered and it can still be played today; see for example the linked video: link.
Moving 1500 Kilometers East of the Burnt City, we get to the next destination in our hunt for Polyhedra in History: The Indus Valley Civilization (IVC), the earliest known urban culture of the Indian sub-continent. This civilization lasted from 3300 BCE to 1300 BCE.
A cubical die from the Mature Harappan phase (2600-1800 BCE) with 1 to 6 dots was found in the rubble during archaeological excavations done in Harappa (one of the largest cities in the IVC) between 1995 and 2001 (ref 10).

Another die made of Terracotta (with dimensions 3.2x3.2x3.2 (cm)) was found in Harappa and is currently at display in the Lahore Museum (Lahore, Pakistan). It was crafted sometime between 2600 BCE to 1900 BCE.

John Hubert Marshall (Director General of the Archaeological survey of India from 1902-1928) who oversaw various excavations in the Indus Valley area writes: "dicing was a common game at Mohenjo-Daro and this is proved in the number of pieces that were found".
The dice found at Harappa were made out of various materials including Terracotta, White Limestone, Yellow Agate, Pottery, Faience, Grey stone. But, most of them they were made out of Terracotta or out of pottery, in the latter case, the clay with which they were made was light red in color, well baked and sometimes coated with a red wash. In one of the Terracotta examples, the dots in the dice were inlaid with tiny beads. The dice were usually cubical, ranging in size from 1.2 by 1.2 by 1.2 (inches) to 1.5 by 1.5 by 1.5 (inches).
The archaeological evidence, albeit scanty, directs our attention to South Asia and to the Harappan period for the possible origin of the cubical type of dice.
Contemporaneously, the evidence (even more scantier) also directs us to Tepe Gawra, an ancient Mesopotamian settlement, in the Mosul region of Northwestern Iraq. Here excavations have yielded cubical dice, which dates back to around the same time as the Harappan cubical dice. A few other examples of cubical dice have also been reported from other Mesopotamian sites.
But, comparatively, at two major Harappan cities (Mohenjo-Daro and Harappa) a relatively large number of cubical dice have been found, than has been uncovered in the numerous and contemporaneous sites in all of Mesopotamia (ref 11).
Although games and the use of dice was popular throughout Mesopotamia and near Eastern History, it is interesting to note that the use of cubical dice seems to have been a rare (and in some cases late) innovation. Even for Egyptians, the cubical dice were not common until the Graeco-Roman times. Although, isolated examples have been found at Thebes and Amarna, dating to the new kingdom (mid 16th century BCE at the earliest).
Ancient Indian sources also describe another game called Chaupar, which was played with 3 oblong dice (as old as 3rd millennium BCE),16 pieces and a board in shape of a cross. It is similar in shape to the parallelepiped dice that we saw above (ref 12) . It is reasonably clear (given the evidence) that the use of cubical and oblong dice was quite common in Indus valley (Harappan sites). We also found evidence of cubical dice outside of India (for example at Ur and Tepe Gawra in Mesopotamia and Tell el’Amarna in Egypt), but it is not the same for the oblong dice. The oblong dice occur very rarely if at all, outside India in this early period.
Though the Harappan sites of 3rd millennium BCE give us the earliest material evidence of civilization in India. We have no literary texts from that period and we still cannot read the brief messages on the many seals that we have discovered. It is difficult to say how the Indus valley people used their dice. Was it the beginning of an investigation into the field of Polyhedra, or was it just a recreational gaming tool, we don't know.
When we get our first literary texts in India, we find that dice playing was a common failing of the upper classes. The Rig-Veda, which we may reasonably consider to have been in its present form before 1000 BCE, has references to the use of dice, and one of its hymns (Book 10, 34) is a charm to cure an inveterate and unsuccessful gambler of the compulsion to gamble that has ruined him. But, the dice mentioned in Rig Veda, were not cubical (more specifically, not a polyhedron), because the dice used were nuts from the Bibhitaka tree. These nuts are almost round but have five slightly flattened sides.
In the ritualistic literature, following the Rig-Veda, the consecration ceremonies for a king included a game of dice–which the new king must always win–and there was a special officer to take charge of the dice. In the great epic known as the Mahabharata there are two famous instances of kings ruined by gambling.
Given the evidence, It is reasonable to assume that dice were made and used for ritualistic, gaming and gambling purposes. Dice itself was probably not viewed as a Mathematical object belonging to a certain group (example the Platonic solids), because if it was, we would see other examples of Polyhedra, other than the regular hexahedron (cubical dice).
In the entire pre-hellenic history, we see such individual instances of Polyhedra being made and used in very specific contexts. In all of these examples, in order to make these polyhedra, the craftsmen, who crafted these polyhedra would need to be intimately familiar with the geometry of the object they were making. Specifically they probably would have started to consciously realize and abstract out the most basic features of the object that they were crafting. Namely, the number of edges, faces and vertices. For example, in the case of the cubical dice, it is reasonable to assume that they would have abstracted out the fact that the dice has 6 faces. Probably, they would have gone one step further and realized that that it has 8 vertices and 12 edges.
If one were to study and consider these polyhedra as a field of geometry to be rigorously investigated in and of itself, the next natural step is the following: how we can alter these basic features (faces, edges, vertices) to make other such solid objects of different shapes. Following which, one would start grouping similar objects into specific categories.
The pre-hellenic civilizations probably abstracted out basic features of the polyhedra they were crafting (number of: faces, edges and vertices), they did not study polyhedra as a field in and of itself. It were the Greeks of the hellenic period who were the first to perform rigorous Mathematical investigation into polyhedra (describing, naming, categorizing).
We will circle back to Greeks in great detail in: Polyhedra in History-2, the second post in the Polyhedra in History series, which is almost entirely devoted to Greeks, who contributed extensively towards the development of the field of Polyhedra for a millennia.
Now we move on to the final part of this post, the Etruscans civilization, who probably preceeded (but not by a long time period) the Greeks in their awareness in at least some of the polyhedra.
The Etruscans were the people of ancient Italy and covered a territory, at its greatest extent, of roughly what is now Tuscany, western Umbria, and northern Lazio, as well as parts of what are now the Po Valley, Emilia-Romagna, south-eastern Lombardy, southern Veneto, and Campania. Etruscan culture was influenced by ancient Greek culture and it endured (starting from around 900 BCE) till the 27 BCE, after which the Etruscan territory was completely into the newly established Roman Empire (as a consequence of the Roman-Etruscan wars).
Excavations at the ancient stone huts of Monte Loffa, near Padua, in Sant'Anna del Faedo village of Breonio (in the region of the western Lessini Mountains) revealed an "almost" regular dodecahedron (believed to be from around 500 BCE) made of soapstone, with Pentagonal faces carved in with figures (ref 13). Stefano De' Stefani was the name of the researcher who found this Dodecahedron.

A Dodecahedron is any polyhedron with 12 flat faces. The most familiar Dodecahedron is the regular Dodecahedron, with 12 copies of a regular pentagon as its faces. The dodecahedron found in Monte Loffa is described as an "almost" regular dodecahedron The faces are pentagons, but of the 12, some of the pentagons might not be regular, hence the "almost" in its description. Still, it is quite close to a regular dodecahedron. A sketch of the regular dodecahedron is shown below, along with that is one of my puzzle shaped like a regular dodecahedron.
The region in which the Etruscan Dodecahedron was found is called by ancient historians as the region of the Reti and Euganei, who were destroyed and scattered by the Gauls. De’ Stefani (in agreement with several ancient writers) considers Reti an ancient Italic people of Etruscan origin, that under the Gaul's pressure had to find refuge on Alps.
Several scholars were interviewed by De’ Stefani, and he came to the conclusion that
this dodecahedron was a die. The paper reports the opinion of Ariodante Fabretti ( 1816-1894, an Italian politician and historian), that De’ Stefani received in a letter written by Carlo Cipolla (1854-1916, another Italian Historian). Fabretti says that it is a dice, and further writes:
"The signs are conventional, perhaps a sort of numerals. In this case, this specimen is interesting because it seems to show a mixture of dots, as in our modern dice, and Etruscan numbers, adapted from the Greek numerals. On one of the face we can see “IV”, may be, for “four” ".
Pythagoras (570 BCE - 495 BCE) is usually credited with the discovery of the Dodecahedron. Given the Dodecahedron found at Monte Loffa, it is debatable whether it were the Etruscans or the Greeks who first discovered the it. But, whoever it was they were not too far apart in their discoveries.
The southern part of Italy, where the Pythagorean school is situated is particularly rich in Pyrite deposits. Commonly referred to as fool's gold, Pyrite the most common sulphide and today its main use is as a source of sulphur for the production of sulphuric acid.
Pyrite usually forms cubic crystals, however in some cases it can also form a shape almost the same as a regular dodecahedron. The shape goes by the name Pyritohedron, which like the regular dodecahedron has 12 identical pentagonal faces, but the difference is that these faces are no longer constrained to be regular pentagons. They can be irregular pentagons, but still they are irregular in the exact same way. Even though the individual crystals have grown into each other, it is still possible to identify the dodecahedral forms.
It is likely that these eye-catching Pyrite crystals may have attracted the attention of Etruscans and Pythagoreans alike, and may have served as an initial inspiration for making and studying these solids.
Although the definition of Pyritohedron requires the 12 irregular pentagons to be identical, we hardly find such examples in nature (although we come quite close). So, given that one in thinking about Pyrite crystals, one should remember that, they are irregular dodecahedron, but not exactly a Pyritohedron.
An Icosahedron is any polyhedron with 20 flat faces. The regular Icosahedron is a polyhedron in which all of the 20 faces are identical equilateral triangles. Fabretti showed to Cipolla an Icosahedron that could have some link to the Etruscan Dodecahedron.
I should mention that, the following part is taken from a conversation, I am not certain whether such an icosahedron exists. It is still worth mentioning because if it does exist, it could be the earliest physical evidence of Icosahedron. The icosahedron was made of blue-glazed earthenware. On each face there were impressed some Greek letters. According to Fabretti, the Icosahedron was owned by the city of Turin, before coming to the Museum of Antiquities, on occasion of an exchange. It was therefore supposed that this object was found in Piedmont.
I will write to the Museum of Antiquities (and accordingly update the blog post), to enquire whether they possess such an Icosahedron from the Etruscan times. We will learn more about the Icosahedron in the second part of this series of blog posts.
This brings us to the end of Part 1 of this series of blog post. To summarize, we covered the following: the Megalithic cuboidal pillars of Göbekli Tepe (9500 BCE), frustum shaped Egyptian Mastabas (5000 BCE) moving forward to the Tetrahedral accounting tokens from Mesopotamia (4000 BCE), Carved stone balls from Neolithic era in Scotland (4000 BCE), the right triangular prism shaped staircase of the Ziggurats (~2600 BCE), the Egyptian (square base) pyramids (~2600 BCE), Tetrahedral dice from Mesopotamia (2600 BCE), Cubical and Oblong dice from the Indus valley civilization (2500 BCE), finally ending at the Dodecahedral dice of the Etruscans (~500 BCE).
In doing so we learnt through historical examples about the following Polyhedra families :Hexahedrons, Frustums, Prisms, Pyramids (Square base Pyramid, Tetrahedron), (Parallelepipeds and Regular Hexahedron), Dodecahedron. Three of the the polyhedra in these families, namely: the Regular Tetrahedron, the Regular Hexahedron, the Regular Dodecahedron are 3 of the 5 platonic solids (as we saw in my introductory blog post).
The remaining 2 platonic solids, that we did not cover in detail in this post are: the Regular Octahedron and the Regular Icosahedron. I will cover them (and much more) in the next part (Part 2) of the Polyhedra in History series of blog post, in which we will begin with exploring Greeks and the plethora of contributions they made towards the study of Polyhedra. Stay tuned!
References
ref 1: Regular Polytopes (book), author: H.S.M Coxeter
ref 2: Özgan, S.Y., Özkar, M. A Thirteenth-Century Dodecahedron in Central Anatolia: Geometric Patterns and Polyhedral Geometry. Nexus Netw J19, 455–471 (2017). https://doi.org/10.1007/s00004-017-0341-0
ref 3: Frank J. Swetz (The Pennsylvania State University), "Mathematical Treasure: Mesopotamian Accounting Tokens," Convergence (September 2012), DOI:10.4169/loci003901
ref 6: Khufu (Wikipedia)
ref 7: Polyhedra (book), Author: Peter R. Cromwell, Cambridge University Press
ref 8: Page 23 in the book Polyhedra by Peter R. Cromwell, Cambridge University Press (1997)
ref 9: History of Mathematics Project, Article: Burnt City Dice
ref 10: Ancient Indus Dice, more information on Harappa.com blog
ref 11: Dales, George F. “Of Dice and Men.” Journal of the American Oriental Society, vol. 88, no. 1, 1968, pp. 14–23. JSTOR, www.jstor.org/stable/597890. Accessed 14 Aug. 2021.
ref 12: Norman Brown, .W."The Indian Games of Pachisi, Chaupar, and Chausar" Expedition Magazine 6.2 (1964): n. pag. Expedition Magazine. Penn Museum, 1964 Web. 14 Aug 2021 <http://www.penn.museum/sites/expedition/?p=729>
ref 13: An Etruscan Dodecahedron, author: Amelia Carolina Sparavigna, Department of Applied Science and Technology Politecnico di Torino, C.so Duca degli Abruzzi 24, Torino, Italy
Image Credits (in order of appearance)
Göbekli Tepe site (South View): Copyright DAI, Author: N. Becke
Göbekli Tepe project building D: Copyright: DAI, Göbekli Tepe project; Author: Göbekli Tepe project.
Stabilisation work on pillar 18, in building D (as seen in 2011): Copyright: DAI, Göbekli Tepe project; Author; Göbekli Tepe project.
Altar in a Tarxien temple: By Ethan Doyle White - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=64453443
A dolmen of Menga: By Grez - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=3727601
A dolmen of North Caucasus: CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=232919
Ġgantija Temple: By Bs0u10e01 - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=76551045
Mastaba image: By Jon Bodsworth - www.egyptarchive.co.uk, Copyrighted free use, https://commons.wikimedia.org/w/index.php?curid=2316988
Mastaba Schematic: Mastaba.jpg: Unknown. Originally uploaded by Oesermaatra0069 at 2006-03-12.derivative work: Master Uegly (talk) - Mastaba.jpg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=15962446
Prismatoid diagram: By Steven Baltakatei Sandoval - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=81640652
Mesopotamian Accounting tokens: Image by Denise Schmandt-Besserat and the University of Pennsylvania Museum of Archaeology and Anthropology, University of Pennsylvania, Philadelphia. Copyright: University of Pennsylvania.
Clay Tablets (Susa, Iran): Image by Denise Schmandt-Besserat and Musée du Louvre, Département des Antiquités Orientales, Paris. Copyright: Musée du Louvre.
Carved stone balls: Image by Ashmolean Museum. Copyright: Ashmolean Museum, University of Oxford.
Step Pyramid of Djoser: By Charles J. Sharp - Own work, from Sharp Photography, sharpphotography, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=32434567
Great Ziggurat of Ur: By Hardnfast, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=3544015
Ur's Ziggurat reconstruction schematic: By user:wikiwikiyarou - Own work, based on a 1939 drawing by Leonard Woolley, Ur Excavations, Volume V. The Ziggurat and its Surroundings, Figure 1.4 [1][2], Public Domain, https://commons.wikimedia.org/w/index.php?curid=923322
Step Pyramid at Monte d'Accoddi, Sardinia (Italy): By Gianni Careddu - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=24854049
Bent Pyramid: By lienyuan lee, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=54566893
Red Pyramid: By Olaf Tausch - Own work, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=36358297
The Great Pyramid of Giza: By Nina - Own work, CC BY 2.5, https://commons.wikimedia.org/w/index.php?curid=282496
Moscow Mathematical Papyrus: By Stumps - wikimedia, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=4997129
Ruins of the town of Ur: By M.Lubinski from Iraq,USA. - Flickr, CC BY-SA 2.0, https://commons.wikimedia.org/w/index.php?curid=3065765
Royal Game of Ur board and Dice: Image by the British Museum, Copyright: The trustees of the British Museum, under Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0) license.
Ruins of Shahr-e-Sukhteh: By Saeedrahdari (سعید راهداری) - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=61499765 .
Burnt city gaming board images and sketches: Images, Copyright (need to further verify): the History of Mathematics project.
Burnt City, Grave 731: Images by Piperno and Salvatori (1983).
Shahr-e-Sukhteh Parallelepiped Dice illustration (markings depicted): Image by History of Mathematics project, Copyright: Wolfram.
Harappa Granary and great hall: By Muhammad Bin Naveed - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=35609614
Mohenjo-Daro excavated ruins: By Saqib Qayyum - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=31519718
Harappan Cubical dice: Image taken from Harappa.com
Another Harappan cubical dice (Terracotta): Image taken from Google Arts and Culture, Lahore Museum section.
Etruscan Dodecahedron from Monte Loffa (along with its 2d net showing all of its 12 faces): Image taken from the following paper: An Etruscan Dodecahedron, author: Amelia Carolina Sparavigna.
Pyritohedron shaped crystal: By Rob Lavinsky, iRocks.com – CC-BY-SA-3.0, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=10154084
Another Pyritohedron shaped crystal: By Didier Descouens - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=6361844
Additional Resources
Explore the faces of a four-valued die from the Burnt City and incrementally morph it from its long skinny box shape to a modern six-sided cubical die: https://www.wolframcloud.com/obj/2173b55c-e1cb-44e0-b09b-f2fe4ce6ee6f
Mathigon timeline of Mathematics: https://mathigon.org/timeline
"Tepe Gawra Excavations." Museum Bulletin V, no. 5 (March, 1935): 34-36. Accessed August 14, 2021. https://www.penn.museum/sites/bulletin/1521/
Brunswig, Robert H. “Radiocarbon Dating and the Indus Civilization: Calibration and Chronology.” East and West, vol. 25, no. 1/2, 1975, pp. 111–145. JSTOR, www.jstor.org/stable/29756054. Accessed 14 Aug. 2021.
Article: Basis for determining the age of the Indus Valley Civilization

































































Comments